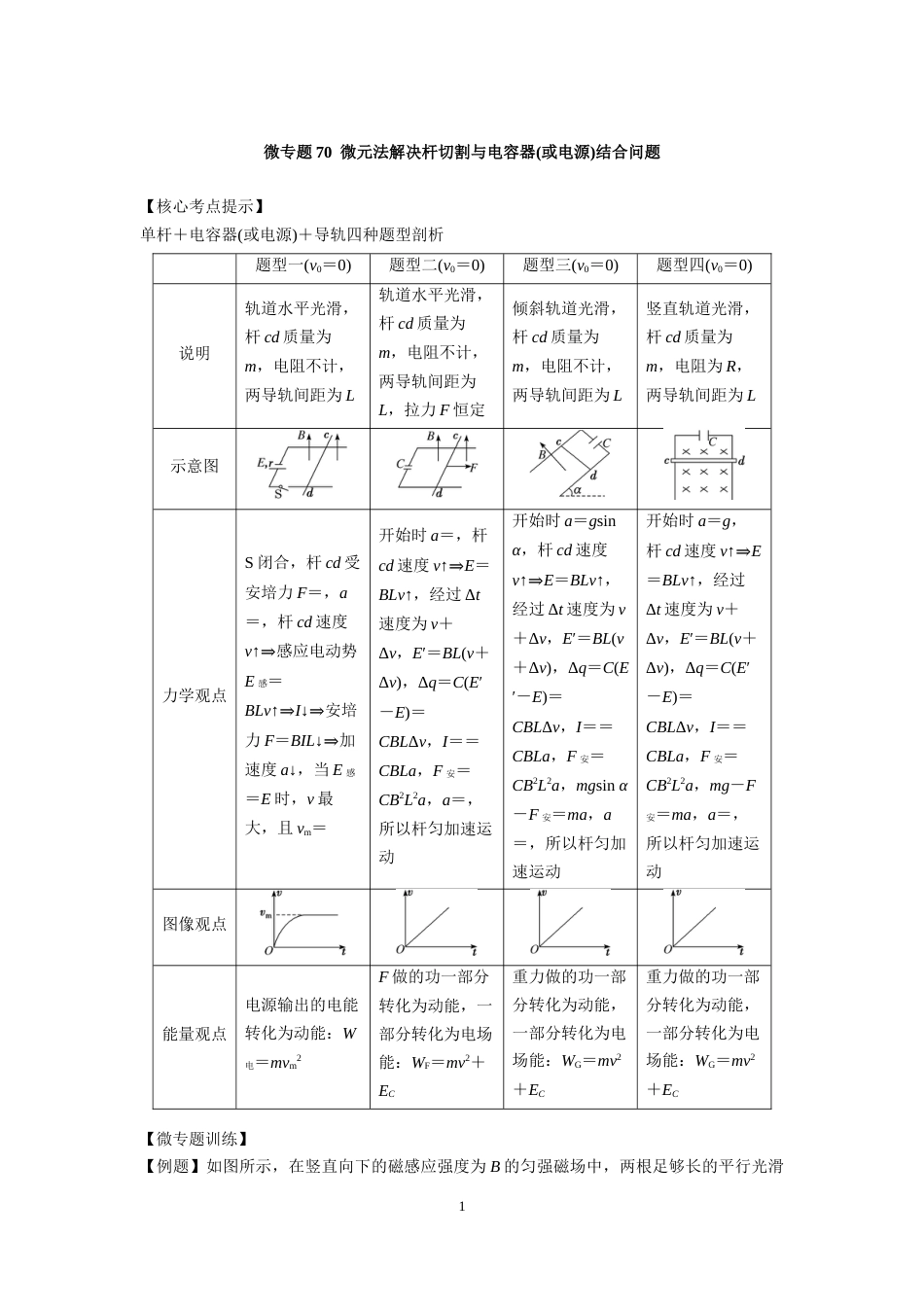
微专题70 微元法解决杆切割与电容器(或电源)结合问题

微专题70微元法解决杆切割与电容器(或电源)结合问题【核心考点提示】单杆＋电容器(或电源)＋导轨四种题型剖析题型一(v0＝0)题型二(v0＝0)题型三(v0＝0)题型四(v0＝0)说明轨道水平光滑，杆cd质量为m，电阻不计，两导轨间距为L轨道水平光滑，杆cd质量为m，电阻不计，两导轨间距为L，拉力F恒定倾斜轨道光滑，杆cd质量为m，电阻不计，两导轨间距为L竖直轨道光滑，杆cd质量为m，电阻为R，两导轨间距为L示意图力学观点S闭合，杆cd受安培力F＝，a＝，杆cd速度v↑⇒感应电动势E感＝BLv↑⇒I↓⇒安培力F＝BIL↓⇒加速度a↓，当E感＝E时，v最大，且vm＝开始时a＝，杆cd速度v↑⇒E＝BLv↑，经过Δt速度为v＋Δv，E′＝BL(v＋Δv)，Δq＝C(E′－E)＝CBLΔv，I＝＝CBLa，F安＝CB2L2a，a＝，所以杆匀加速运动开始时a＝gsinα，杆cd速度v↑⇒E＝BLv↑，经过Δt速度为v＋Δv，E′＝BL(v＋Δv)，Δq＝C(E′－E)＝CBLΔv，I＝＝CBLa，F安＝CB2L2a，mgsinα－F安＝ma，a＝，所以杆匀加速运动开始时a＝g，杆cd速度v↑⇒E＝BLv↑，经过Δt速度为v＋Δv，E′＝BL(v＋Δv)，Δq＝C(E′－E)＝CBLΔv，I＝＝CBLa，F安＝CB2L2a，mg－F安＝ma，a＝，所以杆匀加速运动图像观点能量观点电源输出的电能转化为动能：W电＝mvm2F做的功一部分转化为动能，一部分转化为电场能：WF＝mv2＋EC重力做的功一部分转化为动能，一部分转化为电场能：WG＝mv2＋EC重力做的功一部分转化为动能，一部分转化为电场能：WG＝mv2＋EC【微专题训练】【例题】如图所示，在竖直向下的磁感应强度为B的匀强磁场中，两根足够长的平行光滑1金属轨道MN、PQ固定在水平面内，相距为L。一质量为m...