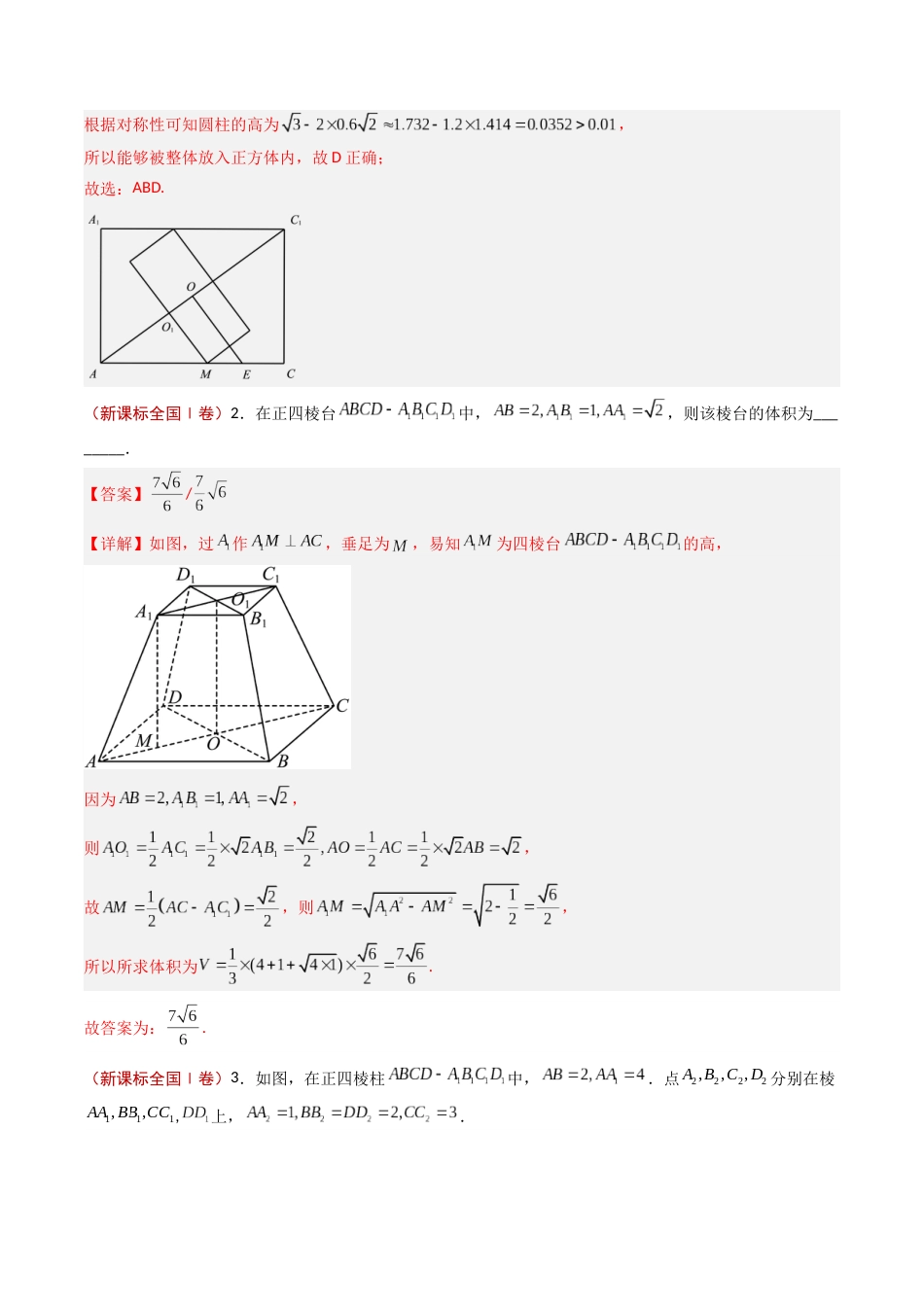
专题13 空间向量与立体几何- 2023年高考真题和模拟题数学分项汇编（全国通用）（解析版）

专题13空间向量与立体几何（新课标全国Ⅰ卷）1．下列物体中，能够被整体放入棱长为1（单位：m）的正方体容器（容器壁厚度忽略不计）内的有（）A．直径为的球体B．所有棱长均为的四面体C．底面直径为，高为的圆柱体D．底面直径为，高为的圆柱体【答案】ABD【详解】对于选项A：因为，即球体的直径小于正方体的棱长，所以能够被整体放入正方体内，故A正确；对于选项B：因为正方体的面对角线长为，且，所以能够被整体放入正方体内，故B正确；对于选项C：因为正方体的体对角线长为，且，所以不能够被整体放入正方体内，故C正确；对于选项D：因为，可知底面正方形不能包含圆柱的底面圆，如图，过的中点作，设，可知，则，即，解得，且，即，故以为轴可能对称放置底面直径为圆柱，若底面直径为的圆柱与正方体的上下底面均相切，设圆柱的底面圆心，与正方体的下底面的切点为，可知：，则，即，解得，根据对称性可知圆柱的高为，所以能够被整体放入正方体内，故D正确；故选：ABD.（新课标全国Ⅰ卷）2．在正四棱台中，，则该棱台的体积为________．【答案】/【详解】如图，过作，垂足为，易知为四棱台的高，因为，则，故，则，所以所求体积为.故答案为：.（新课标全国Ⅰ卷）3．如图，在正四棱柱中，．点分别在棱,上，．(1)证明：；(2)点在棱上，当二面角为时，求．【答案】(1)证明见解析；(2)1【详解】（1）以为坐标原点，所在直线为轴建立空间直角坐标系，如图，则，，，又不在同一条直线上，.（2）设，则，设平面的法向量，则，令，得，，设平面的法向量，则，令，得，，，化简可得，，解得或，或，.（新课标全国Ⅱ卷）4．已知圆锥的顶点为...